|
Feladat
|
A szimuláció szükséges és lehetséges
Az ember természeténél fogva törekedett a világ jelenségeinek, objektumainak és azok összefüggéseinek megismerésére. A tudomány fejlődése során a matematika vált azzá az eszközzé, amely alkalmas ezen tapasztalatok leírására. A matematika eszközrendszerét tehát úgy alakították ki, hogy alkalmas legyen a természet, a gazdaság és a társadalom összefüggéseinek megfogalmazására. A matematika tehát az a nyelv, amely az objektumok, jelenségek - természetüktől függetlenül történő – leírására alkalmas.
A matematika lehetővé teszi az összefüggések egzakt módon való megfogalmazását, ami biztosítja, hogy az adott objektumról, jelenségről annak jelenléte nélkül is ismereteket szerezzünk.
Ezek az összefüggések és a nem kevésbé fontos, napjaink számítógépei által biztosított számítási kapacitás minden eddiginél bonyolultabb problémák megoldását teszik lehetővé.
Fontos a biztonság
Vannak olyan rendszerek, jelenségek, amelyek közvetlen tanulmányozása veszélyes volna. Oktatási céllal veszélyes lenne vizsgálatokat végezni egy atomreaktor belsejében, kerülni szoktuk az erősen mérgező vagy robbanásveszélyes anyagokkal való kísérletezést is.
Anyagi megfontolások
Bizonyos jelenségeket azért nem tudunk közvetlenül megvizsgálni, mert a kísérlethez szükséges anyagok, eszközök túlságosan drágák, vagy más ok miatt nehezen beszerezhetők. A kémiatanárok általában csak megemlítik, hogy a királyvíz oldja az aranyat, de magát a kísérletet általában nem mutatják be. Extrém körülmények (magas nyomás, hőmérséklet, stb.) biztosítása általában szintén drága kísérleti berendezéseket igényel. Máskor az teszi költségessé a kísérletezést, hogy túlságosan sokszor kell elvégezni.
A változás sebessége
Sok esetben a jelenségeket kísérő változások pillanatszerűek, máskor pedig kivárhatatlanul lassúak lehetnek (gyors mechanikai mozgások, kémiai láncreakciók, evolúciós fejlődés, kontinensek vándorlása).
A rendszer összetettsége
Előfordulhat, hogy a vizsgált rendszer túlságosan összetett. Ekkor a vizsgálat szempontjából fontos feltételek biztosítása általában lehetetlen. Ez a probléma állhat elő társadalmi jelenségek vagy ökológiai rendszerek vizsgálatakor.
Etikai korlátok
Az állatokon és embereken végzett kísérletek etikai korlátokba ütközhetnek. Sok estben tehát arra van szükség, hogy élő szervezeteket modellezzünk.
A modellalkotás szakaszai
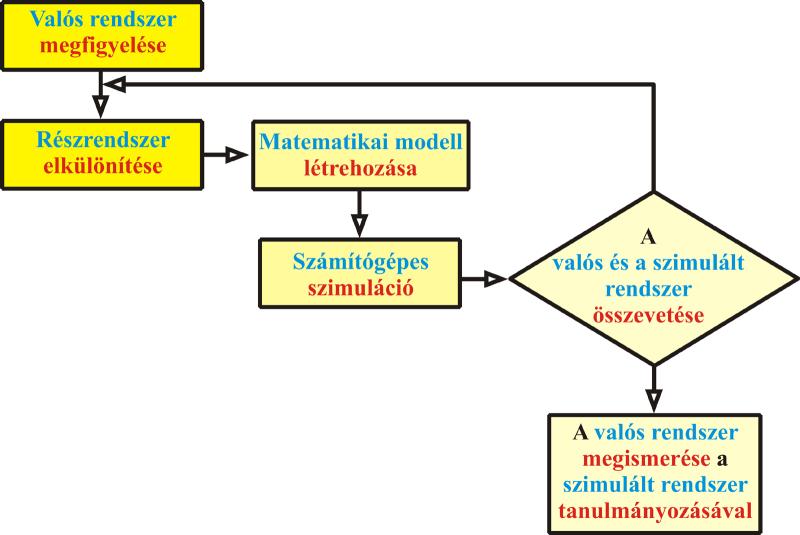
A modellalkotás alapja minden esetben a valóság. A valós rendszer általában túlságosan összetett, pontos matematikai leírása bonyolult volna, de általában szükségtelen is. Az esetek többségében elegendő a valós rendszer egy részének modellezése. Természetesen nem hagyhatunk figyelmen kívül a megismerés szempontjából fontos részleteket. A megfelelő részrendszer elkülönítése után, a megfigyelések alapján elkészítjük annak matematikai modelljét, amelyben megfogalmazzuk az azt leíró összefüggéseket. Az ezek alapján készült számítógépes program a választott részrendszer számítógépes modellje.
A program használatának (számítógépes szimuláció) eredményét összevetjük a valós rendszer viselkedésével. Ha a szimuláció eredményes, azaz a kívánt pontossággal közelíti a valós rendszert, akkor helyesnek fogadjuk el a modellt, és alkalmas a valós rendszer (adott keretek között történő) megismerésére. Ellenkező esetben a matematikai modell további finomítást igényel.
Valamely természeti, gazdasági, társadalmi, stb. rendszer viselkedését leíró olyan matematikai összefüggések összességét, amelyeket a vizsgált rendszer megfigyelése révén hoztunk létre, a rendszer matematikai modelljének nevezzük.
A modellalkotáshoz általában kevesebb információ áll rendelkezésre, mint amivel a valós rendszer teljesen leírható volna, tehát a valóságot csak bizonyos szempontból közelíti megfelelően.
A modell alkotásának, a modellezésnek valójában az a célja, hogy a modell felhasználásával a valós rendszer azon tulajdonságaira is tudjunk következtetni, amelyeket a valóságban nem áll módunkban megfigyelni.
Ez a folyamat a szimuláció.
Tehát a modell készítésének célja maga a megismerés.
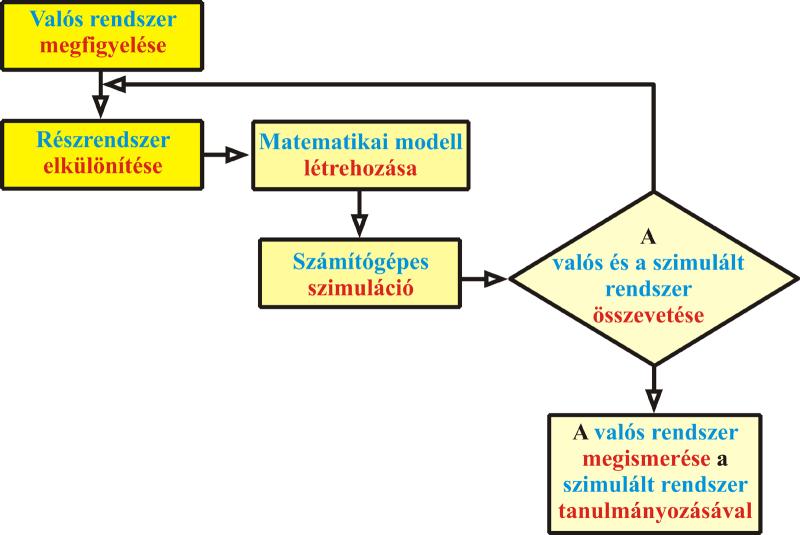
A megismerés folyamata
A megismerés folyamatában nagy szerepe van a természetes, illetve kísérleti körülmények között lezajló változások megfigyelésének. A megfigyelések során összegyűjtött adatok kiértékelése révén fogalmazhatunk meg összefüggéseket, szabályokat, törvényeket.
A modellalkotás szerepe a megismerésben
A megfigyeléseket gyakran szimulációval egészítjük ki. A szimuláció során szerzett tapasztalatokat is fölhasználjuk a valós rendszer megismerésében.
A modellel leírt rendszerre a környezete által gyakorolt hatást, a rendszer mindenkori állapotát és a rendszer hatását a környezetére a rendszer változóival tudjuk jellemezni. Ezek olyan mennyiségek, amelyek megadják a rendszer és környezete közötti anyag- és energiaátadás mértékét, valamint jellemzik állapotát.
A zárt rendszernek csak állapotváltozói vannak. Ha egy rendszernek bemeneti és/vagy kimeneti változói vannak, akkor a rendszer nyílt.
Autonóm rendszernek nincsenek bemeneti változói, a külvilág nincsen rá hatással. Ha ilyen modellt készítünk, akkor elhanyagoljuk a külvilágnak a rendszerre gyakorolt hatását.
Emlékezet nélküli rendszernek nincs állapotváltozója.
A modellezés tárgya
A modelleket csoportosíthatjuk a modellezett rendszer jellege szerint. Így beszélhetünk például
kémiai
fizikai
biológiai
társadalmi
gazdasági, stb.
modellekről.
A modellezés célja
A modellezés alapvető célja minden esetben a valós rendszer megismerése. A megismerés azonban más és más céllal történhet. Fontosak az oktatási céllal készült modellek. Gyakran készítenek modelleket azért, hogy valamely rendszer jövőbeli állapotára következtessenek.
A modell megvalósulása
Anyagi modellről akkor beszélünk, ha a matematikai modell alapján elkészítjük a valós rendszer valamiféle „másolatát”. Megvalósítása idő- és munkaigényes. Szemléltetés vagy kísérletezés céljára meg szokták építeni járművek, épületek kicsinyített mását.
Ha a modell jellemzői nem öltenek testet valami konkrét tárgy formájában, gondolati modellről beszélünk. Ilyenek a számítógépes modellek is.
A változók értékkészlete
Beszélhetünk diszkrét, folytonos és kevert állapotú modellekről aszerint, hogy változói milyen értékeket vehetnek fel.
A modell időfüggése
Időfüggő modell esetében legalább egy változója változik az idő függvényében. Ha ez nem teljesül, időfüggetlen modellről beszélünk, amely lehet statikus vagy dinamikus.
Időfüggő modell esetében van értelme megkülönböztetni diszkrét és folytonos idejű modelleket.
A kimeneti változók függése
Determinisztikus modell esetében a modellezés eredményét a bemenetek és a kezdőállapot egyértelműen meghatározzák.
Sztochasztikus modell esetében a bemenetek és a kezdőállapot csupán a lehetséges kimenetek halmazát esetleg azok eloszlását határozzák meg.
Pictures